Question

by himself, a person can mow his lawn in 80minutes. If his daughter helps, they can mow the lawn together in 60minutes. How long would it take his daughter to mow the lawn by herself.

Answer 1

The father mows the lawn in 80 min.

The father and the daughter mow the lawn in 60 min.

Let "x" represent the time it takes the daughter to mow the lawn by herself.

Express both times as rates:

The dad's mow rate is:

`\frac{1\text{lawn}}{80\min }`

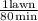
Combined mow rate:

`\begin{gathered} \frac{1\text{lawn}}{80\min}+\frac{1\text{lawn}}{x}=\frac{1\text{lawn}}{60\min } \\ (1)/(80)+(1)/(x)=(1)/(60) \end{gathered}`

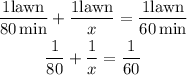
From this expression you can determine the value of x:

- Subtract 1/80 to both sides of the expression

`\begin{gathered} (1)/(80)-(1)/(80)+(1)/(x)=(1)/(60)-(1)/(80) \\ (1)/(x)=(1)/(240) \end{gathered}`

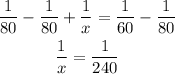
-Raise both sides by -1 to invert the fractions:

`\begin{gathered} ((1)/(x))^(-1)=((1)/(240))^(-1) \\ x=240 \end{gathered}`

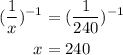
It will take her 240 minutes to mow the lawn by herself.