Question

2.3 kg wooden block is at rest on a frictionless surface. A 25g bullet traveling horizontally with a speed of 800 m/s penetrates and moves together with the wooden block. What is their velocity in m/s?

Answer 1

`\begin{equation*} 8.60\text{ }m\/s \end{equation*}`

Step-by-step explanation

Parameters given:

Mass of the block, M = 2.3 kg

Mass of the bullet, m = 25 g = 0.025 kg

Initial velocity of the block, U = 0 m/s

Initial velocity of the bullet u = 800 m/s

Final velocity of the bullet and the block = v

The bullet and the block will have the same final velocity since they move together. To find the final velocity of the bullet and the block, apply the conservation of momentum:

`mu+MU=(m+M)v`

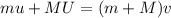
Solving for v, we have that the final velocity of the block and the bullet is:

`\begin{gathered} (0.025*800)+(2.3*0)=(0.025+2.3)v \\ 20=2.325v \\ \Rightarrow v=(20)/(2.325) \\ v=8.60\text{ }m\/s \end{gathered}`

That is the answer.