Question

I have to repost this because I was giving wrong answers. The instructions are to complete each proof using the properties of equality ​

Answer 1

Answer and Step-by-step explanation:

We are given:

`(2y-1)/(-3) = 5`

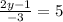
First, we multiply both sides by -3.

2y - 1 = 15

Now we add 1 to both sides.

2y = 16

Finally, we divide by 2 to each side.

y = 8

We are given:

2x + 30 = -4(5x -2)

First we distribute the -4 to 5x and -2.

2x + 30 = -20x + 8

Now we subtract 8 from both sides.

2x + 22 = -20x

Now we subtract 2x from both sides.

22 = -22x

Finally, we divide by -22 to both sides.

-1 = x

Statements: Reasons:

Given

2y - 1 = 15 Multiplication Property of Equality

2y = 16 Addition like terms

y = 8 Division Property of Equality

Statements: Reasons:

2x + 30 = -4(5x -2) Given

2x + 30 = -20x + 8 Distribution Property of Equality

2x + 22 = -20x Subtraction Property of Equality

22 = -22x Subtraction Property of Equality

-1 = x Division Property of Equality

#teamtrees #WAP (Water And Plant)