Question

a scientist have two solutions which she has labeled solution a and solution B each contain salt she knows that solution a is 70% salt and solution B is 95% so she wants to obtain 160 oz of a mixture that is 75% so how many ounces of each solution should she use

Answer 1

Solution:

Let x = the number of ounces of Solution A

Let y = the number of ounces of Solution B

then we have the system of the equation:

x + y = 160 EQUATION 1

0.70 x + 0.95 y = 0.75(160) = 120 EQUATION 2

Solving for y in equation 1, we obtain:

y = 160-x EQUATION 3

replacing the above on equation 2, we get:

0.70 x + 0.95(160-x) = 120

this is equivalent to:

0.70 x + 152 - 0.95x = 120

this is equivalent to

152-120 = 0.95 x -0.70 x

this is equivalent to:

32 = 0.25 x

solving for x, we get:

`x\text{ = }(32)/(0.25)\text{ = 128 }`

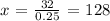
now, replacing the above into the equation 3, we obtain:

y = 160-x = 160 - 128 = 32

then, we can conclude that the correct answer is:

x = the number of ounces of Solution A = 128 ounces

y = the number of ounces of Solution B = 32 ounces.