Question

Real Life Application: Page 30 Q 102 An open box of maximum volume is to be made from a square piece of material 24 cm on a side by cutting equal squares from the corners and turning up the sides (see figure). a. Write volume V as a function of x, the length of the corner squares. a. What is the domain of the function?

Answer 1

The image below will be needed to find the volume function

From the image above, we can see that the dimensions of the open box are

`(24-2x)* x*(24-2x)`

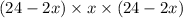
Therefore, the volume function V is given as

`V(x)=(24-2x)* x*(24-2x)`

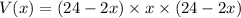
Thus,

`\begin{gathered} V(x)=x(4x^2-96x+576) \\ V(x)=4x^3-96x^2+576x \end{gathered}`

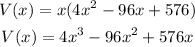
The volume function V is given by V(x) = 4x³ - 96x² + 576x

The domain of V is the values of x for which V is defined for this problem.