The image below will be needed to find the volume function
From the image above, we can see that the dimensions of the open box are
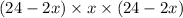
Therefore, the volume function V is given as
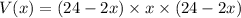
Thus,
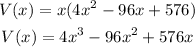
The volume function V is given by V(x) = 4x³ - 96x² + 576x
The domain of V is the values of x for which V is defined for this problem.