Question

Modern oil tankers weigh over a half-million tons and have lengths of up to a quarter of a mile. Such massive ships require a distance of 5.0 km (about 3.0 mi) and a time of 22 min to come to a stop from a top speed of 26 km/h. What is the magnitude of such a ship's average acceleration in m/s2 in coming to a stop? What is the magnitude of the ship's average velocity in m/s? Comment on the potential of a tanker running aground

Answer 1

Acceleration = (change in speed) / (time for the change)

Change in speed= (0 - 26 km/hr) = -26 km/hr

(-26 km/hr) x (1,000 m/km) x (1 hr / 3,600 sec) = -7.222 m/sec

Average acceleration = (-7.222 m/s) / (22 min x 60sec/min) = -0.00547 m/sec²

Average speed during the stopping maneuver =

(1/2) (start speed + end speed) = 13 km/hr = 3.6111 m/sec

Chances of running aground:

If he stays in the designated shipping lanes, he ought to be OK.

Answer 2

Average acceleration,
`a=-7.71* 10^(-5)\ m/s^2`

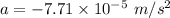
Average velocity, v = 13 km/h

Explanation:

It is given that,

Initial velocity of ship, v = 26 Km/h

Final velocity of ship, u = 0

Distance covered by ship, d = 5 km

Time taken, t = 22 min = 0.36 h

(a) Average acceleration,
`a=(v-u)/(t)`

`a=(0-26\ km/h)/(0.36\ h)`

`a=-72.2\ km/h^2=-7.71* 10^(-5)\ m/s^2`

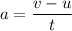
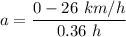
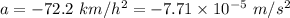
So, the magnitude of ship's acceleration is
`a=-7.71* 10^(-5)\ m/s^2`.

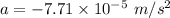(b) Average velocity,
`v_a=(v+u)/(2)`

`v_a=(26\ m/s+0)/(2)`

`v_a=13\ km/h`

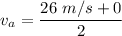
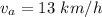
So, ship's average velocity is 13 km/h.

Hence, this is the required solution.