Question

Suppose an investment of $1,800 doubles in value every 7 years. How much is the investment worth after 42 years?

Answer 1

x=2^n(1800)
x=2^6(1800)
x=$115,200

Answer 2

The investment in 42 years will become $115199.88

Explanation:

Let the investment model is
`A=Pe^(rt)`

A = final amount

P = initial amount

r = rate

t = time

Now, given that

P = $1800

A = 2P = 2×1800 = $3600

t = 7 years

`3600=1800e^(7r)\\\\2=e^(7r)\\ln2=7r\\r=(1)/(7)\ln2\\\\r=0.099021`

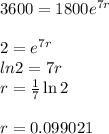
Now, we have to find A for t = 42 years

`A=1800e^(42*0.099021)\\\\A=115199.88`

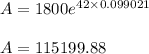
Hence, the investment in 42 years will become $115199.88