Question

Write a formula for the maximum number of segments determined by n points

Answer 1

Let n = the number of points
(x-1) + ... (x-x)

The last term will always be 0, when you reach that, stop.

ex. 1pt: 1-1=0
2pt: (2-1) + (2-2) = 1
3pt: (3-1) + (3-2) + (3-3) = 3

Answer 2

⇒Number of Points in the Plane = n

→There are two Possibility

Either All Points are Collinear, that is Lie Along a Line.

Or, They are, Non- Collinear.

To Determine a segment we need two distinct points.

If All "n" Points are Collinear,Distinct Number of Segment=1

If there are two points in plane, number of Distinct Segment

`=_(2)^(2)\textrm{C}\\\\=(2!)/((2-2)! * 2!)\\\\=1`

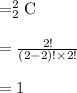
If there are three points in plane, number of Distinct Segment

`=_(2)^(3)\textrm{C}\\\\=(3!)/((3-2)! * 2!)\\\\=3`

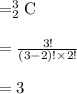
If there are Four points in plane, number of Distinct Segment

`=_(2)^(4)\textrm{C}\\\\=(4!)/((4-2)! * 2!)\\\\=6`

............................................................................................

..................................................................................

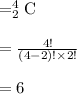
⇒So,If Points are Not Collinear,that is there are "n" points in the plane, then Distinct number of Segment

`=_(2)^(n)\textrm{C}\\\\=(n!)/(2!* (n-2)!)\\\\=(n *(n-1))/(2)`