Question

$800 is deposited in an account that pays 9% compounded semi-annually. Find the balance after 4 years.

Answer 1

Principal = $ 800

Time = 4 years

Rate of Interest = 9% compounded Semi Annually

`=(9\pr)/(2)`

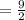
Time = 4× 2=8 periods

As, we have to find balance after 4 years, so we will use the formula for amount in terms of Compound interest.

Amount(A)

`A=P[1+(R)/(100)]^n\\\\ A=800* [1+(9)/(200)]^8\\\\ A=800 * [(209)/(200)]^8\\\\ A=800 * (1.045)^8\\\\ A=800 * 1.422\\\\ A=1137.680`

Balance after 4 years = $ 1137.68

Answer 2

The formula for compound interest is the following:

A=P(1+r/n)^nt
A=accumulated amount (what we're looking for)
P=Principal amount (initial amount). $800 in this case
r=rate. 0.09 in this case which we get from converting 9% to decimal by dividing by a 100.
n=number of times interest is compounded. In this case semi-annually which means 2
t=time. In this case 4 years
Let's calculate:
A=800(1+0.09/2)^(2*4)
A=800(1+0.045)^8
A=800(1.045)^8
A=800(1.42210061284)
A=1137.68049027
Let's round to the hundredth place (to represent cents) since the amount represents money.
Answer=The balance after 4 years will be $1,137.68