Question

James paddles upstream in a canoe at 2mph (relative to the shore), and when he paddles down-stream, he goes 9mph. Find the speed of the current and the speed James can paddle in still water and come up with an equation.

Answer 1

Not sure what equation you're looking for, but against the current he goes 2 mph and with he goes 9mph, so 9-2=7mph difference between them, divided by 2 = 3.5 mph of the current. So in this case, James can paddle 2+3.5= 5.5 mph in still water and the current moves at 3.5 mph.


James can paddle 5.5 mph
The current moves at 3.5 mph
Equation: speed = 5.5 + 3.5x where x can equal -1, 0, or 1 depending on whether James is going with the current (x = 1), without the current (x = 0), or against the current (x = -1)

Answer 2

Let x represent James's speed and y represent the speed of the current. Since upstream the current goes against him,
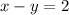
`x-y=2` describes the speed upstream, and since downstream the current goes with him,
`x+y=9` describes the speed downstream.

Use elimination to solve for x:
`x-y=2 \\ -(x+y=9) \\ =-2y=-7 \\ y=7/2` or 3.5 miles per hour for James in still water. Substitute y into either original equation:
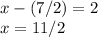
`x-(7/2)=2 \\ x=11/2` or 5.5 miles per hour for the current. As far as an equation, you can use
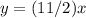
`y=(11/2)x`, where x is the number of hours James has paddled in still water and y is the distance he has traveled (in miles).