Help plz i’m unsure how to do this. Plato

Question

asked Aug 21, 2023 156k views

1 Answer

Retendo · Answer 1 · 2023-08-26T19:07:12+0000

Answer:

C

Explanation:

Standard form of a Parabola that facing downwards, with focus, p and vertex (h,k)

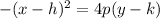
$- (x - h) {}^(2) = 4p(y - k)$

We know the vertex is (-4,-3) so we get

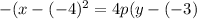
$- (x - ( - 4) {}^(2) = 4p(y - ( - 3)$

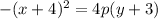
$- (x + 4) {}^(2) = 4p(y + 3)$

Now we need to find the length of the focus.

The focus length is 1 because the distance from the vertex to focus is 1 so p=1

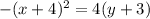
$- (x + 4) {}^(2) = 4(y + 3)$

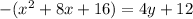
$- ( {x}^(2) + 8x + 16) = 4y + 12$

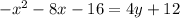
$- {x}^(2) - 8x - 16 = 4y + 12$

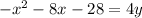
$- {x}^(2) - 8x - 28 = 4y$

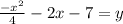
$\frac{ - {x}^(2) }{4} - 2x - 7 = y$

C is the answer