Question

Is this an even or odd function? f(x)=5-3x

Answer 1

`f(x)=5-3x \\ x \in \mathbb{R}`

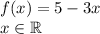
A function is even if f(x)=f(-x) for every x in the domain.

`f(x) \stackrel{?}{=} f(-x) \\ 5-3x \stackrel{?}{=} 5-3 * (-x) \\ 5-3x \stackrel{?}{=} 5+3x \\ -3x-3x \stackrel{?}{=} 5-5 \\ -6x \stackrel{?}{=} 0 \\ x \stackrel{?}{=} 0 \\ f(x)=f(-x) \Leftrightarrow x=0`
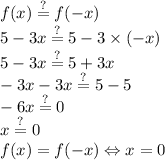
f(x) is equal to f(-x) if and only if x=0, so the function isn't even.

A function is odd if -f(x)=f(-x) for every x in the domain.

`-f(x) \stackrel{?}{=} f(-x) \\ -(5-3x) \stackrel{?}{=} 5-3 * (-x) \\ -5+3x \stackrel{?}{=} 5+3x \\ 3x-3x \stackrel{?}{=} 5+5 \\ 0 \stackrel{?}{=} 10 \\ 0 \\ot= 10 \\ -f(x) \\ot= f(-x)`
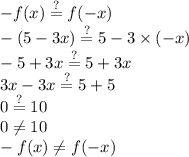
-f(x) is never equal to f(-x), so the function isn't odd.

The function is neither even nor odd.