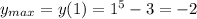Question

Ex 2.8
3. find the maximum value of y for the curve y=x^5 -3 for -2≤x≤1

Answer 1

`y=x^5-3\\ y'=5x^4\\\\ 5x^4=0\\ x=0\\ 0\in [-2,1]\\\\ y''=20x^3\\\\ y''(0)=20\cdot0^3=0`

The value of the second derivative for
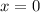
`x=0` is neither positive nor negative, so you can't tell whether this point is a minimum or a maximum. You need to check the values of the first derivative around the point.
But the value of
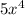
`5x^4` is always positive for
`x\in\mathbb{R}\setminus \{0\}`. That means at
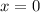
`x=0` there's neither minimum nor maximum.
The maximum must be then at either of the endpoints of the interval
`[-2,1]`.
The function
`y` is increasing in its entire domain, so the maximum value is at the right endpoint of the interval.


`y_(max)=y(1)=1^5-3=-2`