Question

1. what is the GCF of the terms of 8c^3+12c^2+10c?

A.2
B.4
C.2c
D.4c


2. How can the polynomial 6d^4+9d^3-12d^2 be factored l?

Answer 1

If you pay attention 2 goes into 8, 10, & 12 and it looks like they all have one C. So what do you think it is lol?(:

Answer 2

1. C. 2c

2.
`3d^2(2d^2+3d-4)`

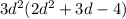
Explanation:

A. We have been given an expression and we are asked to find the GCF of our given expression.

`8c^3+12c^2+10c`

Let us find factors of each of our given terms.

Factors of
`c^3` are
`c*c*c`,

Factors of
`c^2` are
`c*c`,

We can see that c is the greatest common factor of
`c^3`,
`c^2` and
`c`.

Factors of 8 are: 1, 2, 4, 8.

Factors of 12 are: 1, 2, 3, 4, 6, 12.

Factors of 10 are: 1, 2, 5, 10.

The greatest common factor of 8,12 and 10 is 2.

So let us factor out 2c from our expression.

`2c(4c^2+6c+5)`

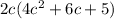
Therefore, the greatest common factor of our given expression is 2c and option C is the correct choice.

2. We have been given a polynomial and we are asked to factor our given polynomial.

`6d^4+9d^3-12d^2`

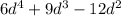
We will pull out the greatest common factor of the terms of our given polynomial.

We can see that GCF of
`d^4`,
`d^3` and
`d^2` is
`d^2`.

The GCF of 6, 9 and 12 is 3.

So let us factor out
`3d^2` from our polynomial.

`3d^2(2d^2+3d-4)`

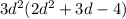
Therefore, the factored form of our given polynomial is
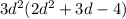`3d^2(2d^2+3d-4)`.