Question

Please help!

Which point is collinear with points B and C?



A.
(0, 0)

B.
(1, 1)

C.
(1, –5)

D.
(6, –8)

Answer 1

Points are collinear if they lie on the same line.

First find the equation of the line that passes through the points B and C.

`B(4, -3) \\ x_1=4 \\ y_1=-3 \\ \\ C(-4,3) \\ x_2=-4 \\ y_2=3 \\ \\ m=(y_2-y_1)/(x_2-x_1)=(3-(-3))/(-4-4)=(3+3)/(-8)=(6)/(-8)=-(3)/(4) \\ \\ y=-(3)/(4)x+b \\ (-4,3) \\ 3=-(3)/(4) * (-4)+b \\ 3=3+b \\ b=0 \\ \\ y=-(3)/(4)x`

The points lie on the line y=(-3/4)x.
Now plug the coordinates of the given points into the equation and check if they satisfy the equation.


`(0,0) \\ x=0 \\ y=0 \\ \Downarrow \\ 0 \stackrel{?}{=} -(3)/(4) * 0 \\ 0 \stackrel{?}{=} 0 \\ 0=0 \\ \hbox{the point lies on the line} \\ \\ (1,1) \\ x=1 \\ y=1 \\ \Downarrow \\ 1 \stackrel{?}{=} -(3)/(4) * 1 \\ 1 \stackrel{?}{=} -(3)/(4) \\ 1 \\ot= -(3)/(4) \\ \hbox{the point doesn't lie on the line}`


`(1,-5) \\ x=1 \\ y=-5 \\ \Downarrow \\ -5 \stackrel{?}{=} -(3)/(4) * 1 \\ -5 \stackrel{?}{=} -(3)/(4) \\ -5 \\ot= -(3)/(4) \\ \hbox{the point doesn't lie on the line} \\ \\ (6,-8) \\ x=6 \\ y=-8 \\ \Downarrow \\ -8 \stackrel{?}{=} -(3)/(4) * 6 \\ -8 \stackrel{?}{=} -(9)/(2) \\ -8 \\ot= -(9)/(2) \\ \hbox{the point doesn't lie on the line}`

The answer is A.

Answer 2

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Coordinates of B = (4,-3)

Coordinates of C = (-4,3)

We need to find the collinear point with B and C.

There is one method to find the collinear point i.e. Slope method.

Slope of BX = Slope of CX =
`(y_2-y_1)/(x_2-x_1)`

Let Coordinates of X = (0,0)

So, Slope of BX is given by

`(0+3)/(0-4)=(3)/(-4)`

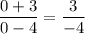
Slope of CX is given by

`(0-3)/(0+4)=(-3)/(4)`

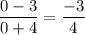
So, Slope of BX = Slope of CX =
`(-3)/(4)`

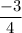
And we can see from the graph (0,0) is the collinear point with B and C too.

Hence, Option 'A' is correct.