We have the next diagram
In order to have the system in equilibrium, we will analyze the torque on the pivot
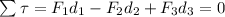
In this case
F1=0.155(9.8)
F2=0.025(9.8)
F3=0.275(9.8)
The distances
d1=50-18.5=31.5cm=0.315 m
d2=50-38.4=11.6cm=0.116 m
We substitute
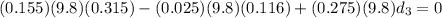
then we isolate the d3

d3=0.188m=18.8cm
From the beginning of the uniform meter stick will be 50+18.8=68.8cm
ANSWER
d3=18.8cm
From the beginning of the uniform meter is 68.8cm