Let's assume we have a base value of K and we are told that it depreciates an average of p% each year. The value V(t) after t years is given by the following exponential function:
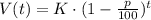
In this case K is the original value of the car $39367, p is the percentage of depreciation i.e. 22. Then the value of the car bought by Brianna t years after she bought it is:
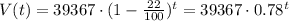
Then the approximate value in 9 years will be V(9):
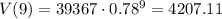
We need to round it to the nearest dollar so the answer is $4207.