Question

What's the solution set for the inequality x^2-2x<8?

Answer 1

`x^2-2x<8\\x^2-2x-8<0\\(x-4)(x+2)<0`

So, the numbers to base your solution set on are -2 and 4 (the numbers that the equation equal to 0)

Then, you plug in 3 numbers to the equation: a number less than -2, a number between -2 and 4, and a number greater than 4. They represent the three sections of the number line created by the points -2 and 4. So, our numbers will be -3, 0, and 5:


`(x-4)(x+2)<0\\(-3-4)(-3+2)<0\\(-7)(-1)<0\\7<0`

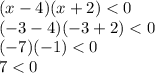
7<0 is incorrect, so the section of the number line less than -2 does not work.


`(x-4)(x+2)<0\\(0-4)(0+2)<0\\(-4)(2)<0\\-8<0`

-8<0 is correct, so the section of the number line between -2 and 4 works.


`(x-4)(x+2)<0\\(5-4)(5+2)<0\\(1)(7)<0\\7<0`

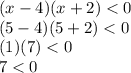
7<0 is incorrect, so the section of the number line above 4 does not work.

So, only the section between -2 and 4 works. However, the problem is a "less than" problem, not a "less than or equal to" problem, so -2 and 4 are not included in the solution set. That gives you the answer:

(-2, 4) (NOT BRACKETS because -2 and 4 are not included)