Question

Write the equation of the parabola in vertex form, factored form, and general form.

Answer 1

The vertex form of the parabola is

`y=(x-1)^2-4`

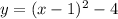
the general form is

`y=x^2-2x-3`

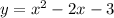
and the factored form is

`y=(x+1)(x-3)`

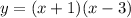
To solve this, we look at the graph and see that the vertex coordinates are (1,-4)

the vertex form is

`y=a(x-h)^2+k`

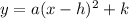
where h is the x coordinate of the vertex and k is the y coordinate. now we have to find the value of a

the factor form is

`y=a(x-x_1)(x-x_2)`

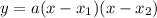
where x1 and x2 are the roots of the parabola. we know the coordinates of the roots: (-1,0) (3,0)

now, we can use this to find the value of a

`y=a(x+1)(x-3)`

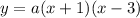
now we plug the coodinates of the vertex (1,-4) in the equation before and solve for a

`-4=a(1+1)(1-3)`

`(-4)/(-4)=1=a`

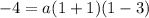
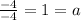
now we just add the value of a to the factor and vertex forms. the only thing remaining is the general form. for this we need to apply the distributive property in the factor form

`y=(x+1)(x-3)=x^2-2x-3`

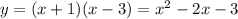
and thus, we have all three forms calculated