The vertex form of the parabola is
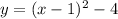
the general form is
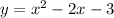
and the factored form is
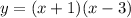
To solve this, we look at the graph and see that the vertex coordinates are (1,-4)
the vertex form is
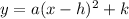
where h is the x coordinate of the vertex and k is the y coordinate. now we have to find the value of a
the factor form is
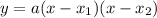
where x1 and x2 are the roots of the parabola. we know the coordinates of the roots: (-1,0) (3,0)
now, we can use this to find the value of a
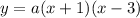
now we plug the coodinates of the vertex (1,-4) in the equation before and solve for a
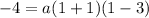
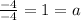
now we just add the value of a to the factor and vertex forms. the only thing remaining is the general form. for this we need to apply the distributive property in the factor form
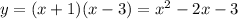
and thus, we have all three forms calculated