Question

Identify intervals on which the function is increasing, decreasing, or constant.

g(x) = 4 - (x - 6)2 (2 points)


A. Increasing: x < 4; decreasing: x > 4

B. Increasing: x < 6; decreasing: x > 6

C. Increasing: x < -6; decreasing: x > -6

D. Increasing: x > 4; decreasing: x < 4

Answer 1

The answer is B.

Explanation:

The formula is;

`g(x)=4-(x-6)^2`

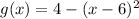
Maximum value of the function is where the x value makes (x-6)^2 equals to 0. Then;

`(x-6)^2=0\\x=6`

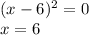
Breaking point of the function is x=6. When we put 6 instead of x, the function will go to:

`g(6)=4-(6-6)^2\\g(6)=4`

When we put x=4, the function will go to;

`g(4)=4-(4-6)^2=4-2^2=0`

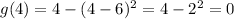
Then the solution is increasing: x < 6; decreasing: x > 6

Also check the graph at the attachment.