Solution
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given geometric series
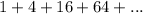
STEP 2: Write the formula to calculate the sum of nth terms of a geometric series
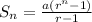
where r is the common ration
a is the first term
Sn is the sum of the nth term
n is the number of terms
STEP 3: Write the required data values
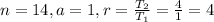
STEP 4: substitute the values to find the sum of the first 14 terms
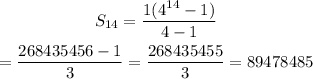
Hence, the sum of the first 14 terms of the given geometric series is 89478485