Question

Find the sum of the first 14 terms of the geometric series 1+4+16+64+….

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given geometric series

`1+4+16+64+...`

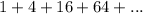
STEP 2: Write the formula to calculate the sum of nth terms of a geometric series

`S_n=(a(r^n-1))/(r-1)`

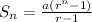
where r is the common ration

a is the first term

Sn is the sum of the nth term

n is the number of terms

STEP 3: Write the required data values

`n=14,a=1,r=(T_2)/(T_1)=(4)/(1)=4`

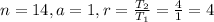
STEP 4: substitute the values to find the sum of the first 14 terms

`\begin{gathered} S_(14)=(1(4^(14)-1))/(4-1) \\ =(268435456-1)/(3)=(268435455)/(3)=89478485 \end{gathered}`

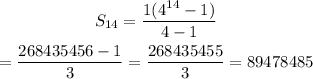
Hence, the sum of the first 14 terms of the given geometric series is 89478485