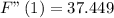Question

Functions defined by integrals, graphing calculator required. Please let me know if you have any questions regarding the materials, I'd be more than happy to help. Thanks!

Answer 1

The important detail here is to remember the fundamental theorem:

`\int_a^bf\mleft(x\mright)dx=F\lparen b)-F\left(a\right)`

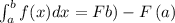
There F is the primitive of f, but what happens when we take the derivative of F? We get f, then

`(d)/(dx)F\left(x\right)=f\mleft(x\mright)`

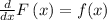
It's very important!

Let's say that know we have a function by integral, like

`\int_0^xf\mleft(t\mright)dt`

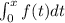
Using our theorem and the derivative

`(d)/(dx)\int_0^xf\lparen t)dt=(d)/(dx)F\lparen x)-(d)/(dx)F\left(0\right)`

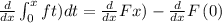
Therefore!

`(d)/(dx)\int_0^xf\mleft(t\mright)dt=f\mleft(x\mright)`

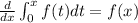
That's the important property here!

After this quick introduction let's solve our problem, in fact, let's do it step by step because we can do small errors.

`F\left(x\right)=\int_0^(2x)\tan\mleft(t^2\mright)dt`

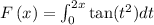
The problem asks for the value of the second derivative at 1! but first, let's find the first derivative, remember that

`F\left(x\right)=\int_0^(2x)\tan\mleft(t^2\mright)dt=G\left(2x\right)-G\lparen0)`

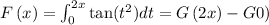
Then if we do the derivative we get

`F^(\prime)\left(x\right)=(d)/(dx)G\left(2x\right)-(d)/(dx)G\left(0\right)`

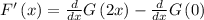
Where G is the primitive of tan(t²). Look at the right side, see that we must apply the chain rule on one term and the other term is constant, G(0) is a number then its derivative is zero! Hence

`F^(\prime)\left(x\right)=(d)/(dx)G\left(2x\right)`

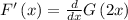
Apply the chain rule

`F^(\prime)\left(x\right)=2G^(\prime)\left(2x\right)`

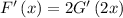
Now let's just use the fact that

`G^(\prime)\left(t\right)=\tan\mleft(t^2\mright)`

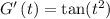
Then we can already solve the derivative! Where we have t we will input 2x

`F^(\prime)\left(x\right)=2G^(\prime)\left(2x\right)=2\tan\mleft(4x^2\mright)`

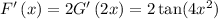
Now we already know the first derivative!

`F^(\prime)\left(x\right)=2\tan\mleft(4x^2\mright)`

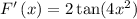
Now we have the first derivative, we will do the derivative again, then

`F^{^(\prime)^(\prime)}\left(x\right)=(d)/(dx)\lparen2\tan(4x^2))`

Apply the chain rule again and remember that d/dx of tan(x) is sec²(x)

`F^{^(\prime)^(\prime)}\left(x\right)=16x\cdot\sec^2\mleft(4x^2\mright)`

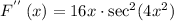
Therefore the second derivative is

`F^{^(\prime)^(\prime)}(x)=16x\sec^2(4x^2)`

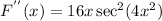
We want to evaluate it at x = 1, which means F''(1), then

`F^(\prime)^(\prime)\lparen1)=16\sec^2\left(4\right)`

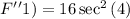
Now we must use the calculator to evaluate sec²(4), if we use our calculator to do it we find

`\begin{gathered} F`

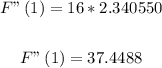
Then the final result is

`F`