Answer:
10 units
Explanation:
Let the shortest side be x
Now since we are given that The congruent sides of an isosceles triangle are each 1 unit longer than the length of the shortest side of the triangle.
So, the length of the congruent sides (each) = x+1
Thus the perimeter of triangle = sum of all sides
= x+x+1+x+1
=3x+2
Now we are given that The perimeter of the triangle is the same as the perimeter of a square whose side length is 2 units shorter than the length of the shortest side of the triangle.
Side of square = x-2
So, perimeter of square = 4*side
=4(x-2)
=4x-8
Now since the perimeter of the triangle and square are equal
So,
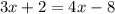

Hence the shortest side of the triangle is 10 units.