Question

(b) The diagram below shows a quadrilateral with the length of its sides written in terms of x. 1.8 (15-2x) cm (3x - 7) cm (2x + 5) cm (i) Write an expression, in terms of x, for the perimeter of the quadrilateral. [2] Express your answer in its simplest form. The perimeter of the quadrilateral is 32 cm. Find the longest side of the quadrilateral. (ii) (2x - 1) cm [2]

Answer 1

Step-by-step explanation

From the image, we will have the sides of the quadrilateral as:

`\begin{gathered} 1)(15-2x)cm \\ 2)(3x-7)cm \\ 3)(2x-1)cm \\ 4)(2x+5)cm \end{gathered}`

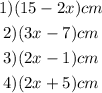
Part I

Therefore, the perimeter of the quadrilateral is the sum of all the sides. This is given as

`\begin{gathered} p=15-2x+3x-7+2x-1+2x+5 \\ group\text{ like terms} \\ p=-2x+3x+2x+2x+15-7-1+5 \\ p=5x+12 \end{gathered}`

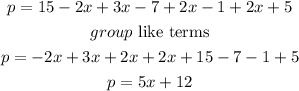
Answer: (5x+12) cm

Part II

Since the perimeter of the quadrilateral is 32cm. Therefore,

`\begin{gathered} 5x+12=32 \\ 5x=32-12 \\ 5x=20 \\ x=(20)/(5)=4cm \end{gathered}`

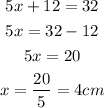
From the image it is clear that the longest side is 2x+5, we can then convert this to its actual length value.

`longest\text{ side =2x+5=}2(4)+5=8+5=13`

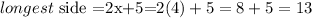
Answer: 13cm