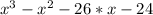Answer:
The answer is x³-x²-26x-24
Explanation:
Firstly, any polynomial can be formed from its roots following the next rule:
Let r1, r2, r3,..., the roots of a polynomial P(x)
P(x)=C*(x-r1)*(x-r2)*(x-r3)*...
Where C is a real constant number excepting zero.
So for roots -4,-1 and 6, the polynomial is:
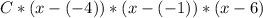
![C*(x+4)*(x+1)*(x-6)\\C*[(x^2+5*x+4)*(x-6)]\\C*[x^3+5*x^2+4*x-6*x^2-30*x-24]\\C*[x^3-x^2-26*x-24]\\](https://img.qammunity.org/2017/formulas/mathematics/high-school/mfjx0ns6ws2r0mrldheoudxz8o57s0f1iy.png)
Finally, considering C=1 (can be any real number excepting zero)