Question

The weekly revenue for a product is given by R(x)=216x−0.033x2, and the weekly cost is C(x)=9000+108x−0.066x2+0.00002x3, where x is the number of units produced and sold.(a) How many units will give the maximum profit?(b) What is the maximum possible profit?

Answer 1

First, we need to find an equation for the profit. The profit is the difference between the revenues R(x) and the costs C(x).

We already know the expressions for R(x) and C(x), so we just need to write R(x) - C(x):

`P(x)=R(x)-C(x)`
`P(x)=216x-0.033x^2-(9000+108x-0.066x^2+0.00002x^3)`

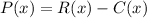
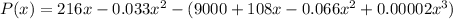
Now we can work the parenthesis:

`P(x)=216x-0.033x^2-9000-108x+0.066x^2-0.00002x^3`

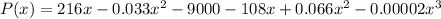
Simplifying like terms:

`P(x)=108x+0.033x^2-0.00002x^3-9000`

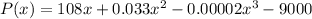
To find the maximum profit we need to calculate the values of x that make the derivative of P(x) = 0.

First, we calculate the derivative:

`P^(\prime)(x)=108+2\cdot0.033x-3\cdot0.00002x^2`
`P^(\prime)(x)=108+0.066x-0.00006x^2=0`

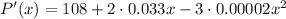
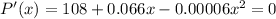
Solving the second-grade equation we obtain that the values making the equation above 0 are 2000 and -900. We can discard -900 as it is a negative number.

Then we have that

a) The number of units that will give the maximum profit is x = 2000.

Now to calculate the maximum possible profit we just need to estimate the profit when 2000 units are produced. That is obtained then by calculating P(2000):

`P(2000)=108\cdot(2000)+0.033\cdot(2000)^2-0.00002\cdot(2000)^3-9000`
`P(2000)=179000`

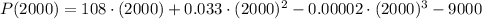
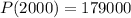
With this we have finally that:

b) The maximum possible profit is 179000.