Question

The specification for a length x is 43.6 cm with a tolerance of 0.1 cm. Write the specification as an absolute value inequality.

Answer 1

`43.5\leq x\leq 43.7`

Explanation:

We have been given that the specification for a length x is 43.6 cm with a tolerance of 0.1 cm. We are asked to write given specification as an absolute value.

`|\text{Actual-Ideal}|\leq \text{Tolerence}`

Upon substituting our given values, we will get:

`|x-43.6|\leq 0.1`

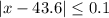
Using absolute value definition
`|x|\leq a=-a\leq x\leq a`, we will get:

`-0.1\leq x-43.6\leq 0.1`

`-0.1+43.6\leq x-43.6+43.6 \leq 0.1+43.6`

`43.5\leq x \leq 43.7`

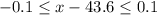
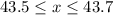
Therefore, our required inequality would be
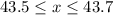`43.5\leq x \leq 43.7`.

Answer 2

My answer to the problem is as follows:

Expressed as an absolute value.

The difference between the actual length, x, and the specification, 43.6, can be no more than 0.1

|x - 43.6| ≤ 0.1 <–––––

The 43.6 is the target length, and the tolerance of 0.1 is how far off from the target is acceptable.