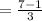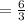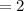Question

The graph of f(x) = 2x + 1 is shown below. Explain how to find the average rate of change between x = 0 and x = 3.

Answer 1

The average rate of change is 2.

Explanation:

If we have a function f(x),

Then the average rate of change in the function from x = a to x = b is,

`(f(b)-f(a))/(b-a)`

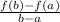
Here, the given function is,

f(x) = 2x + 1 -----(1)

Thus, the average rate of change between x = 0 and x = 3 is,

`(f(3)-f(0))/(3-0)`

From equation (1),

`=((2* 3+1)-(2* 0+1))/(3)`

`=(7-1)/(3)`

`=(6)/(3)`

`=2`

Answer 2

My answer to the problem is as follows:

average rate of change = (f(3) - f(1))/(3-1)

graph 2^x + 1

(1) graph 2^x

(2) move the graph up by 1

I hope my answer has come to your help. God bless and have a nice day ahead!