Question

Solving a percent mixture problem using a linear equationSamantha vEspelTwo factory plants are making TV panels. Yesterday, Plant A produced 7000 fewer panels than Plant B did. Two percent of the panels from Plant A and 3% ofthe panels from Plant B were defective. How many panels did Plant B produce, if the two plants together produced 860 defective panels?Number of panels produced by Plant :Х5?

Answer 1

Number of panels produced by plant B: 20000

Step-by-step explanation

First we have to name the variables. We're looking for the number of panels produced by plant B and also we don't know the number of panels produced by plant A.

Let x be the number of panels produced by plant A and y the number of panels produced by plant B.

We know that plant A produced 7000 fewer panels than plant B. This as an equation is:

`x=y-7000`

To solve this we need to find another equation, because we have two variables.

The other equation is the one with the defective panels. The total number of defective panels produced by both plants is 860, and we know that represents the 2% of produced panels from plant A and 3% of produced panels from plant B. To find the number that represents that percentage we divide the percentage by 100 and multiply by the total amount. For the 2% of plant A this is:

`(2)/(100)\cdot x=0.02x`

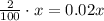
And the 3% of plant B is:

`(3)/(100)\cdot y=0.03y`

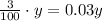
So the second equation is:

`0.02x+0.03y=860`

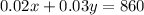
Since we only want to find y, which is the number of panels produced by plant B, we can use the substitution method. Substitute the first equation into the second - in other words, replace x in the second equation by y - 7000:

`0.02(y-7000)+0.03y=860`

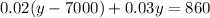
To solve for y, first apply the distributive property of multiplication:

`\begin{gathered} 0.02y-0.02\cdot7000+0.03y=860 \\ 0.02y-140+0.03y=860 \end{gathered}`

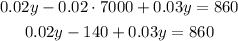
Add like terms:

`\begin{gathered} (0.02y+0.03y)-140=860 \\ 0.05y-140=860 \end{gathered}`

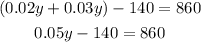
Add 140 on both sides of the equation:

`\begin{gathered} 0.05y-140+140=860+140 \\ 0.05y=1000 \end{gathered}`

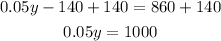
And divide both sides by 0.05:

`\begin{gathered} (0.05y)/(0.05)=(1000)/(0.05) \\ y=20000 \end{gathered}`

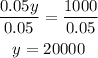
This result means that plant B produced 20000 TV panels in total.