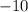Question

A quadratic function has a line of symmetry at x = –3 and a zero at 4.

Q1: What is the distance from the given zero to the line of symmetry?

Q2: What is the other zero of the quadratic function?

Answer 1

Part 1)
`7\ units`

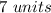
Part 2) The other zero is
`-10`

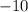
Explanation:

we know that

If the line of symmetry is equal to
`x=-3`

then

the quadratic function is a vertical parabola and the x-coordinate of the vertex is
`-3`

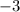
Part 1) What is the distance from the given zero to the line of symmetry?

The distance is equal to the absolute value of the difference of
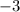`-3` from
`4`

`d=\left|4-\left(-3\right)\right|=7\ units`

Part 2) What is the other zero of the quadratic function?

we know that

In a quadratic function the distance from the zero's to the line of symmetry is equal

so

Subtract
`7` from
`-3`

`-3-7=-10`

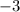
The other zero is
`-10`

Answer 2

I have my hints here on how to solve the questions one and two:

Q1: Just find the distance from -3 to 4. That's 7.

Q2: It is 7 units to the left of -3. Subtract 7 from -3. That's -10

I hope my answer has come to your help. God bless and have a nice day ahead!