Question

Using the given zero, find all other zeros of f(x).

-2i is a zero of f(x) = x4 - 45x2 - 196

Answer 1

The answer is -2i,2i,7,-7.

Explanation:

It is obvious that if -2i is a zero of the function, 2i is also zero of the function. There for (x^2+4) is a factor of the function. If we divide the function to (x^2+4) we will find other factor of the function.

`f(x)/(x^2+4)=(x^4-45x^2-196)/(x^2+4)=x^2-49`

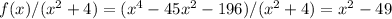
x^2-49 is the other factor of the function. Therefore, +7 and -7 are the other zeros of the function.

Answer 2

The solution to the problem is as follows:

x^4 - 45x^2 - 196 = (x-7)(x+7)(x^2+4),

Therefore, the roots of the given algebraic expression/polynomial are 7,-7,2i,-2i

I hope my answer has come to your help. God bless and have a nice day ahead!