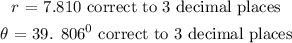Question

I have a trig question about the Cartesian coordinate and converting to polar coordinates Picture included

Answer 1

Step 1:

In this question, we are given the following:

Step 2:

The details of the solution are as follows:

From the question, we can see that the cartesian coordinate:

`(x\text{, y \rparen = \lparen 6, 5 \rparen}`

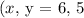
Converting rectangular cordinates to polar co-ordinates, we have that:

`\begin{gathered} \text{x = r cos }\theta \\ y\text{ = r cos }\theta \\ \text{and } \\ \theta\text{ = }\tan^(-1)\text{ \lparen}(y)/(x)) \\ \text{r = }\sqrt{x^2\text{+ y}^2} \end{gathered}`
`\begin{gathered} since\text{ x = 6 and y = 5, we have that:} \\ r\text{ =}\sqrt{6^2+\text{ 5}^2}=\text{ }\sqrt{36\text{ + 25}}=√(61) \\ r\text{ =}√(61)\text{ = 7. 810 \lparen correct to 3 decimal places\rparen} \\ Hence,\text{ r = 7.810 \lparen coreect to 3 decimal places\rparen} \end{gathered}`
`\begin{gathered} \theta\text{ = }\tan^(-1)\text{ \lparen}(y)/(x))\text{ =}\tan^(-1)((5)/(6))\text{ = 39. 806}^0\text{ \lparen correct to 3 decimal places\rparen} \\ Hence,\text{ }\theta\text{ = 39. 806}^0(\text{ correct to 3 decimal places\rparen} \end{gathered}`

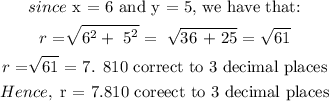
CONCLUSION:

The final answers are:

`\begin{gathered} r\text{ = 7.810 \lparen correct to 3 decimal places\rparen} \\ \theta\text{ = 39. 806}^0\text{ \lparen correct to 3 decimal places\rparen} \end{gathered}`