Question

In ΔABC, if m ∠A = m∠C, m∠B = ß (where ß is an acute angle), and BC = x, which expression gives the length of b, the side opposite ∠B ?

Answer 1

The length of b is
`√(2x^2(1-cos\beta))`.

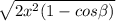Step by step explanation:

Given information: In ΔABC, ∠A =∠C, ∠B = ß (where ß is an acute angle), and BC = x.

Since two angles are same therefore triangle ABC is an isosceles triangle and side AB and BC are congruent.

`AB=BC=x`

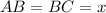
According to Law of cosine

`b^2=a^2+c^2-2ac\cos B`

`b^2=x^2+x^2-2(x)(x)\cos \beta`

`b^2=2x^2-2x^2\cos \beta`

`b^2=2x^2(1-\cos \beta)`

`√(2x^2(1-cos\beta))`

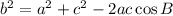
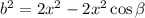
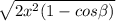
Therefore the length of b is
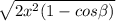`√(2x^2(1-cos\beta))`.