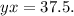Question

Find the constant of variation k for the inverse variation. Then write an equation for the inverse variation.

y = 5 when x = 7.5

Answer 1

An inverse equation follows the formula

y=kxYou're given y=5 ,
x=7.5 plug these values into your equation.
5=k7.5
solve for k.
k=5(7.5)k=37.5
rewrite equation y=37.5x
and now we can check to see if our values are correct
5=37.5/7.5
=5

Hope this helps

Answer 2

Answer: The required constant of inverse variation is 37.5 and equation for the inverse variation is
`yx=37.5.`

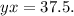
Step-by-step explanation: We are given to find the constant of inverse variation and to write an equation for the following inverse variation :

y = 5 when x = 7.5.

Let k denote the constant of inverse variation.

According to the given information, we can write

`y\propto(1)/(x)\\\\\\\Rightarrow y=(k)/(x)~~~~~~~~~~~~~~~~~~~~~~~~~~~[\textup{k is the constant of inverse variation}]\\\\\Rightarrow yx=k~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

When y = 5, x= 7.5, then from equation (i), we get

`5*7.5=k\\\\\Rightarrow k=37.5.`

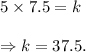
Substituting the value of k in equation (i), we arrive at

`yx=37.5.`

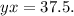
Thus, the required constant of inverse variation is 37.5 and equation for the inverse variation is
`yx=37.5.`