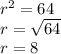Question

The equation for the circle below is x2 + y2 = 64. What is the length of the circle's radius?

Answer 1

Radius of the circle is 8

Explanation:

The equation of a circle is given by

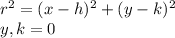`r^2 = (x -h)^2 + (y-k)^2\\y, k = 0 \\` when the cordinate of the circle lies at the center

Thus, the equation of circle becomes

`r^2 = x^2 + y^2\\`

Where,

r is the radius of the circle

Substituting the given values in above equation, we get -

`r^2 = 64\\r = √(64) \\r = 8\\`

Answer 2

First we write equation for circle that consist coordinates of the center and it consists radius. Equation goes like this:

(x-x1)^2 + (y-y1)^2 = r^2

x1 and y1 are coordinates of the center. since the circle's center is at coordinate start that means that (x1,y1) = (0,0)

that means that 64 on the right side of given equation is r^2
r^2 = 64
r = 8

Answer is 8