Question

Find the sum of the first seven terms of the sequence 4, 12, 36, 108,

Answer 1

The numbers are multiplying by 3 each time. For example 4x3=12. 12x3=36 so you would add 4+12+36+108+324+972+2916 = 4373

Answer 2

The sum of first seven term of series is 4372.

Explanation:

We need to calculate the sum of first seven term of given series

Given series is 4, 12, 36, 108,

we can see the pattern of series is each new term is multiplied by 3 with previous term.

4, 12, 36, 108,

This is in the form of geometric series

A geometric sequence has a constant ratio r and is defined by
`a_n=a_0\cdot r^(n-1)`

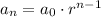
where
`r=3`

`\mathrm{The\:first\:element\:of\:the\:sequence\:is}`
`a_1=4`

`a_n=a_1\cdot r^(n-1)`

`\mathrm{Therefore,\:the\:}n\mathrm{th\:term\:is\:computed\:by}\:`

`r=3,\:a_n=4\cdot \:3^(n-1)`

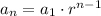
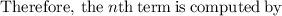
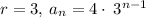
so, 4, 12, 36, 108, 324, 972, 2916,..

`\mathrm{Geometric\:sequence\:sum\:formula:}`

`a_1(1-r^n)/(1-r)`

`\mathrm{Plug\:in\:the\:values:}`

`=4\cdot (1-3^7)/(1-3)=4372`

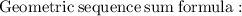
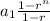
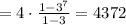
Therefore, the sum of first seven term of series is 4372.