Question

How many extraneous solutions does the equation below have?

Answer 1

Two. m=1.5 and m=-1.5

Answer 2

The equation has:

zero extraneous solution.

( Both are true solution )

Explanation:

We are given a algebraic expression in terms of variable m as:

`(2m)/(2m+3)-(2m)/(2m-3)=1`

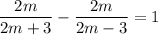
On taking least common multiple we get:

`(2m* ( 2m-3)-2m* (2m+3))/((2m+3)(2m-3))=1`

i.e.

`(4m^2-6m-4m^2-6m)/(4m^2-9)=1\\\\\\(-12m)/(4m^2-9)=1\\\\\\-12m=4m^2-9\\\\\\4m^2+12m-9=0`

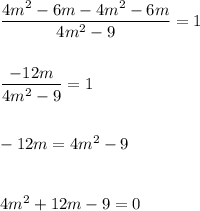
Hence, on solving for m we get:

`m=(-3\pm 3√(2))/(2)`

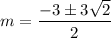
• when
  `m=(-3+3√(2))/(2)`

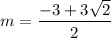
Then,

`(2* (-3+3√(2))/(2))/(2* (-3+3√(2))/(2)+3)-(2* (-3+3√(2))/(2))/(2* (-3+3√(2))/(2)-3)=1\\\\\\(-3+3√(2))/(-3+3√(2)+3)-(-3+3√(2))/(-3+3√(2)-3)=1\\\\\\\\(-3+3√(2))/(3√(2))-(-3+3√(2))/(-6+3√(2))=1\\\\\\(-1+√(2))/(√(2))-(-1+√(2))/(-2+√(2))=1\\\\\\(√(2)-1)((1)/(√(2))-(1)/(√(2)-2))=1\\\\\\(√(2)-1)((√(2)-2-√(2))/((√(2)-2)))=1`

`(-2* (√(2)-1))/((√(2)-2)* √(2)))=1`

`(-√(2)(√(2)-1))/((√(2)-2))=1\\\\\\(√(2)-2)/(√(2)-2)=1\\\\\\1=1`

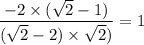
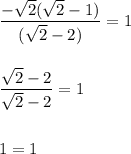
Hence, the solution is a true solution.

• Similarly we may check for:

`m=(-3-3√(2))/(2)`

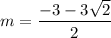
It will also be a true solution.