Question

1. Line FG contains points F (3, 7) and G (−4, −5). Line HI contains points H (−1, 0) and I (4, 6). Lines FG and HI are

parallel

perpendicular

neither

2. Line AB contains points A (8, −4) and B (1, −5). The slope of line AB is

−7

negative 1 over 7

1 over 7

7

Answer 1

1. >> neither
2. >> m=
`- (1)/(7)` >> negative 1 over 7

Answer 2

1. Neither

2. 1 over 7

Explanation:

We know that the formula for slope joining the points
`( x_(1) ,y_(1) )` and
`( x_(2) ,y_(2) )` is given by
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`.

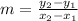1. We have the line FG having end points ( 3,7 ) and ( -4,-5 ). The slope of this line is given by,

`m_(FG)=(-5-7)/(-4-3)`

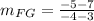
i.e.
`m_(FG)=(-12)/(-7)`

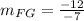
i.e.
`m_(FG)=1.714`

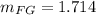
Also, the line HI is given with end points ( -1,0 ) and ( 4,6 ). Its slope is given by,

`m_(HI)=(6-0)/(4+1)`

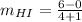
i.e.
`m_(HI)=(6)/(5)`

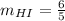
i.e.
`m_(HI)=1.2`

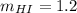
Since, neither the slope of FG and HI are equal nor their product is -1.

Hence, FG and HI are neither parallel nor perpendicular respectively.

2. We have the line AB with end points ( 8,-4 ) and ( 1,-5 ). So, the slope of AB is,

`m_(AB)=(-5+4)/(1-8)`

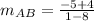
i.e.
`m_(AB)=(-1)/(-7)`

i.e.
`m_(AB)=(1)/(7)`

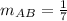
Hence, slope of AB is 1 over 7.