Question

Using the given zero, find all other zeros of f(x).

-2i is a zero of f(x) = x4 - 45x2 - 196

Answer 1

This was hard for me, but I believe I came to the right solutions...

7,-7,2i,-2i

Answer 2

2i, 7 and -7 are the rest of zeros for the function.

Explanation:

The given function is

`f(x)=x^(4)-45x^(2) -196`

The zeros of a function refer to those values that make
`f(x)=0`.

We know by given that one zero is
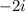`-2i`, that means the second zero must be
`2i`, because complex solutions happen in pairs.

The 2 zeros left can be find by evaluating the function with divisors of the constant term, which are

`1, 2, 4, 7, 14,...`

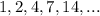
By testing each one of these divisors, we found that numbers 7 and -7 are zeros of the function. (We always use positive and negative divisors)

`f(7)=(7)^(4)-45(7)^(2) -196=2401-2205-196=0=f(-7)`

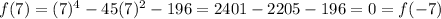
Notice that the function has only pair exponents, that means positive and negative give the same result as you observed above.

Therefore, the other three zeros of the given function are: 2i, 7 and -7.