Question

If x = −2 is a zero of the polynomial function f(x) = 2x3 + 9x2 − 8x − 36, which of the following is another zero of f(x)?

Select one:
a. x = 8
b. x = 4
c. x = 3
d. x = 2

Answer 1

f(x) = 2*x^3 + 9x^2 -8x - 36
= 2x ( x^2 - 4) + 9( x^2 -4)
= (2x + 9)(x^2 - 4)
= (2x + 9)(x-2)(x+2)

x = 2, -2 , -9/2

ans. = d. x=2

Answer 2

Answer: Option d is correct that is x=2 is the another zero of the given polynomial

Step-by-step explanation:

We have been given the polynomial
`2x^3+9x^2-8x-36`

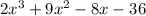
Zero of any polynomial is the point where the value of function is zero

Here we are given one zero at x=-2 if we substitute the value x=-2 in the given polynomial we will get zero

Now to find other point where we will get the solution or we will get zero

First we substitute x=8 in the given polynomial we will get

`2(8)^3+9(8)^2-8(8)-36\\\\=1500\\eq0` Hence, not the zero of given polynomial

Similarly, when we substitute x=4 in the given polynomial we will get

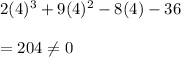`2(4)^3+9(4)^2-8(4)-36\\\\=204\\eq0` Hence, not the zero of given polynomial

Similarly, substitute x=3 in the given polynomial we will get

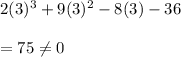`2(3)^3+9(3)^2-8(3)-36\\\\=75\\eq0` Hence, not the zero of given polynomial

Substitute x=2 in the given polynomial we will get

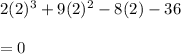`2(2)^3+9(2)^2-8(2)-36\\\\=0` Hence, the zero of the polynomial

Therefore Option d is correct.