Question

An arch is in the shape of a parabola. It has a span of 72 meters and a maximum height of 9 meters.

Answer 1

Equation of the parabola:

`y=-(1)/(144)x^2+9`

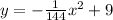
The height of the arch 18 meters from the center is 6.75m

Step-by-step explanation:

The arch feet are 72m apart and the origin half way between them. This means that the axis of symmetry (or the x.coordinate of the vertex) is x = 0

Since it's an arch, the parabola is concave down, with it's maximum at the vertex, y = 9. This means that the vertex is at (0, 9). Also, we can see that the y-intercept is y = 9

Finally, we know the two roots of the parabola: x = -36 and x = 36. This is because the points x = -36 and x = 36 are 72m apart, with the center at the original, as the problem says. SInce x = 36 is a root, this means that at that point the y value is 0.

With all this, we can try to find the general form of a parabola. The general form is:

`y=ax^2+bx+c`

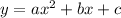
c is the y-intercept. We know that c = 9

We can find the value of b, because we know the coordinates of the vertex. The x-coordinate of the vertex is:

`x_(vertex)=-(b)/(2a)`

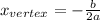
SInce the x-coordinate of the vertex is x = 0

`0=-(b)/(2a)`

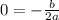
If we solve:

`b=0`

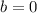
So far we have:

`y=ax^2+9`

Finally, to find a, we can use the point (36, 0) (one of the roots)

`0=a(36)^2+9`

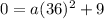
And solve:

`\begin{gathered} 324a=-9 \\ . \\ a=-(9)/(1296)=-(1)/(144) \end{gathered}`

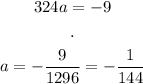
Thus, the equation of the arch is:

`y=-(1)/(144)x^2+9`

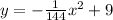
Evaluating this equation for x = 18, we can find the height of the arch:

`y=-(1)/(144)(18)^2+9=-(9)/(4)+9=-6.75`