Question

Theorem: The segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.

A two-column proof of the theorem is shown, but the proof is incomplete.

Which of the following completes the proof?

a. by the addition property
b. by the distance formula
c. by construction
d. given

Answer 1

the answer is
b. by the distance formula (it can be find by using thales distance theorem)

Answer 2

Answer: b. by the distance formula

Explanation:

The Distance Formula is a useful method for finding the distance between two points.

Given points of A=(6,8)

C=(8,4)

Thus, AC=
`√((x_2-x_1)^2+(y_2-y_1)^2)`

`=√((8-6)^2+(4-8)^2)`

`√((2)^2+(-4)^2)`

`√(4+16) =√(20)`

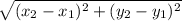
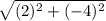
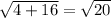
Coordinates of segment DE is given by statement 1.

D=(4,5) and C=(5,3)

DE=
`=√((5-4)^2+(3-5)^2)`

`√((1)^2+(-2)^2)`

`√(1+4) =√(5)`

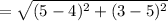
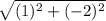
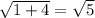
which gives the statement 2.