Question

Use the intermediate value theorem for polynomials to show that the polynomial function has a real zero between the numbers given.f(x)= -8x^5+5x^3-6x^2+1;-1 and 0

Answer 1

The intermediate value theorem for polynomials states that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis.

To prove it has a real zero, it must cross the x-axis.

The theorem thus states mathematically that;

We test for the continuity of the polynomial at x = a and x = b

Hence,

`\begin{gathered} f(a)=f(-1) \\ f(x)=-8x^5+5x^3-6x^2+1 \\ f(-1)=-8(-1^5)+5(-1^3)-6(-1^2)+1 \\ f(-1)=8-5-6+1 \\ f(-1)=-2 \end{gathered}`

`\begin{gathered} f(b)=f(0) \\ f(x)=-8x^5+5x^3-6x^2+1 \\ f(0)=-8(0^5)+5(0^3)-6(0^2)+1 \\ f(0)=1 \\ f(0)=1 \end{gathered}`

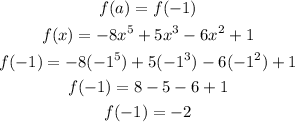
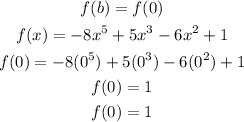
From the above, since the value of the output of the function at the input (intervals) -1 and 0 changes from negative to positive (i.e, from -2 to 1), then it should pass through the x-axis.

Once the function passes through the x-axis, then it will have a real zero between the interval given.