Question

In each figure find the measure of the angles and the lengths of the sides

Answer 1

According to the problem, angles E and F are equal. Angles D and G are equal.

Also, if the trapezoid is isosceles, then FG = DE by definition. So, we express the following

`\begin{gathered} FG=DE \\ 11=a-4 \end{gathered}`

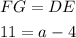
Let's solve for a

`\begin{gathered} 11+4=a \\ a=15 \end{gathered}`

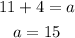
We already know that the sum of all the interior angles is 360°.

`c+c+4c-20+4c-20=360`

Let's solve for c

`\begin{gathered} 10c-40=360 \\ 10c=360+40 \\ c=(400)/(10)=40 \end{gathered}`

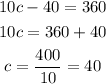
Then, we find each angle using the value of c

`\begin{gathered} D=c=40 \\ G=c=40 \\ E=4c-20=4\cdot40-20=160-20=140 \\ F=4c-20=4\cdot40-20=160-20=140 \end{gathered}`

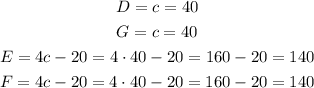
Hence, angles D and G measure 40°, angles E and F measure 140°.