Answer:
Option 3 -
 ; the sum is 72.
; the sum is 72.
Explanation:
Given : The population of a local species of dragonfly can be found using an infinite geometric series where
 and the common ratio is one half.
and the common ratio is one half.
To find : Write the sum in sigma notation and calculate the sum that will be the upper limit of this population.
Solution :
Geometric series is
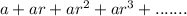
The formula of sum of geometric infinite series is
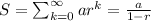
In the given geometric series,
 and
and

According to question,
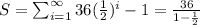
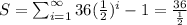

Therefore, Option 3 is correct.
 ; the sum is 72.
; the sum is 72.