According to Bohr's Model of the Hydrogen Atom, the energy of the n-th state is given by the expression:
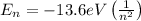
If an electron changes from a state n to a state m, the energy of the photon emitted is given by:
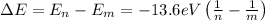
Replace n=6 and m=4 to find the energy of the emitted photon:
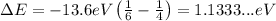
On the other hand, the energy of a photon and its wavelength are related through the equation:
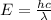
Then, the wavelength of the photon emitted is:
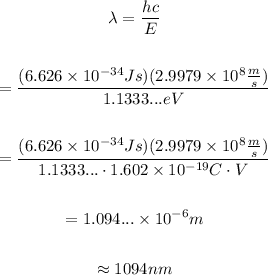
Therefore, the wavelength of the photon emitted is approximately 1094 nanometers.