Question

An electron in the n= 6 state of a hydrogen atom makes a transition to the n= 4 state and emits a photon in the process. What is the wavelength, in nm, of the photon emitted?

Answer 1

According to Bohr's Model of the Hydrogen Atom, the energy of the n-th state is given by the expression:

`E_n=-13.6eV\left((1)/(n^2)\right)`

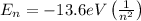
If an electron changes from a state n to a state m, the energy of the photon emitted is given by:

`\Delta E=E_n-E_m=-13.6eV\left((1)/(n)-(1)/(m)\right)`

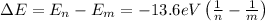
Replace n=6 and m=4 to find the energy of the emitted photon:

`\Delta E=-13.6eV\left((1)/(6)-(1)/(4)\right)=1.1333...eV`

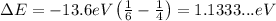
On the other hand, the energy of a photon and its wavelength are related through the equation:

`E=(hc)/(\lambda)`

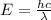
Then, the wavelength of the photon emitted is:

`\begin{gathered} \lambda=(hc)/(E) \\ \\ =((6.626*10^(-34)Js)(2.9979*10^8(m)/(s)))/(1.1333...eV) \\ \\ =((6.626*10^(-34)Js)(2.9979*10^8(m)/(s)))/(1.1333...\cdot1.602*10^(-19)C\cdot V) \\ \\ =1.094...*10^(-6)m \\ \\ \approx1094nm \end{gathered}`

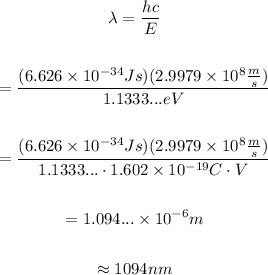
Therefore, the wavelength of the photon emitted is approximately 1094 nanometers.